Denna vecka avslutas vektorkapitlet med:

3.4  Cross Product    och

3.5  Lines and planes in 3-Space.

Dessutom ingår de tre första avsnitten i Kapitel 10 (Komplexa tal):

10.1  Complex Numbers

10.2  Modulus; Complex Conjugate; Division

10.3  Polar Form: DeMoivre's Theorem.

3.4  Cross Product Definitionen av kryssprodukt ges i boken i tre likvärdiga versioner (två st på s. 141 samt en på s.144). Den på s. 144 är troligen den som är lättast att komma ihåg, men den bygger tyvärr på ett sätt att beräkna determinanter som ingår i det uteslutna avsnittet   2.4. Det man behöver veta från 2.4 är dock bara följande: 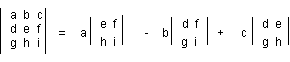En 3x3-determinant kan alltså skrivas som en linjärkombination av 2x2-determinanter. Notera att då 2x2-determinanterna bildas ur de två sista raderna är första radens element faktorer i summans termer. Observera också att mellantermen har negativt tecken. Med denna determinantformel aktuell blir formeln för uxv nederst på s. 144 fullt begriplig. De tre enhetsvektorerna i, j och k förekommer i denna formel. De definieras överst på s. 144: i = (1,0,0),   j = (0,1,0) och k = (0,0,1) . Kryssprodukten uxv bildar alltså en ny vektor som är vinkelrät mot både u och v. På s. 145 förekommer en regel som försöker förklara åt vilket håll uxv pekar i förhållande till u och v. Regeln kallas där 'right-hand rule'. På svenska brukar man tala om 'skruvregeln' som formuleras så här: uxv pekar åt det håll en (normalgängad) skruv rör sig om den skruvas med den rotationsriktning som svarar mot att u rör sig i riktning mot v. Detta är samma regel som den som anger åt vilket håll z-axeln pekar i ett normalt 3-dimensionellt koordinatsystem. Här definieras skruvriktningen av att positiva x-axeln rör sig i riktning mot positiva y-axeln. Några algebraiska regler för kryssprodukten finns formulerade iThm 3.4.1 och 3.4.2. Notera särskilt att    uxv = -vxu. Dessutom är det värt att påpeka att associativitet int gäller allmänt, dvs. det är inte säkert att (uxv)xw = ux(vxw). Kryssprodukten har en hel del intressanta geometriska tolkningar. En sådan ges av formel (6) överst på s. 146: 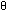||uxv|| = ||u||.||v||sin Detta betyder alltså att ||uxv|| är lika med arean av den parallellogram som spänns upp av u och v. Se figuren på s. 146. En annan viktig geometrisk tolkning tolkning har den s.k. skalära trippelprodukten u.(vxw), även kallad lådprodukten. Den, eller snarare dess belopp, ger nämligen volymen av den parallellepiped som spänns upp av de tre vektorerna i produkten (se figur på s. 149). Lådprodukten har också den trevliga egenskapen att den kan skrivas som en determinant. u.(vxw) är nämligen lika med den determinant vars rader består av i tur och ordning u:s, v:s och w:s komponenter. (Se formel (7) på s. 147.) Ett viktigt specialfall får man då de tre vektorerna ligger i samma plan. I det fallet har ju den uppspända parallellepipeden volymen = 0. Därför får man att lådprodukten (dvs. determinanten som bildas av de tre vektorerna) = 0 om och endast om de tre vektorerna ligger i samma plan. (Thm 3.4.5).

Egenskaper och begrepp Kryssprodukten uxv (Tre versioner av definitionen. Se särskilt determinantvarianten på s. 144). Algebraiska lagar för uxv. (Thm 3.4.1 och 3.4.2) Observera att uxv = -vxu. Skruvregeln som bestämmer uxv:s riktning. (right-hand rule, s. 145). ||uxv|| = arean av den av u och v uppspända parallellogrammen. (Formel (6), s. 146). u.(vxw) = skalära trippelprodukten = lådprodukten, som kan skrivas som en determinant.(s. 147) |u.(vxw)| = volymen av den uppspända parallellepipeden (Thm 3.4.4). Lådprodukten = 0 (dvs. motsvarande determinant = 0) betyder att de tre vektorerna ligger i samma plan, (Thm 3.4.5)

Hemuppgifter 1bc 3a 7 8b 9abc 11bc 12

3.5  Lines and planes in 3-Space.

Detta avsnitt visar hur ekvationerna för linjer och plan kan skrivas på vektorform. Ett plan kan med hjälp av sin normalvektor n beskrivas av ekvationer som de i formlerna (1) och (2) på s. 155, ekvation (3) i Thm, 3.5.1 , s. 156, och (kanske den mest användbara versionen): n.(r - r0) = 0      (ekvation (5), s. 158.) Här är vektorn r0 en konstant vektor som anger en punkt i planet. r är den variabla vektorn som anger en godtycklig punkt i planet. Ekvationen utsäger alltså att vektorn r - r0 (som ligger inbäddad i planet) och planets normalriktning n är vinkelräta. En linje bestäms entydigt av en punkt som ligger på linjen och av den riktning som linjen definierar. Båda dessa element kan beskrivas av vektorer: r0(punkten på linjen) och v (linjens riktning i form av en vektor). I boken anges linjens ekvation på parameterform, (7) på s. 159, där r0:s och v:s komponenter figurerar. I vektorformen: r - r0 = tv         (8), s. 161 uppträder vektorerna själva. En tillämpning som visas (Thm 3.5.2) är formeln för avståndet mellan en punkt och en linje i 3-dimensionella rummet. Som synes är formeln en direkt generalisering av motsvarande formel i 2 dimensioner från avsnitt 3.3 (s. 139).

Egenskaper och begrepp Planets ekvation på komponentform ( (2) s. 155 och (3) s. 156) vektorform n.(r - r0) = 0 ( (5), s.158 ) Linjens ekvation på parameterform ( (7), s.159 ) vektorform r - r0 = tv ( (8) s. 160) Formeln för avståndet mellan en punkt och en linje i 3 dimensioner.

Hemuppgifter 1b 4b 5bc 8a 9b 12bc 39bc

10.1  Complex Numbers

Vi gör alltså nu ett hopp i boken för att läsa om komplexa tal Komplexa tal är numera oundgängliga hjälpmedel i både ren och tillämpad matematik och bör alltså studeras med omsorg. I kursboken gås de viktigaste egenskaperna igenom i de tre första avsnitten av Kapitel 10. I 10.1 definieras de komplexa talen som ett ordnat par av tal, (a,b) som också skrivs a + bi. Här kallas a realdelen och b imaginärdelen. Talen visar sig fungera som 2-dimensionella vektorer i fråga om addition och subtraktion. Ett komplext tal kan alltså tolkas som en punkt i det komplexa planet. Vid multiplikation anges en lag (formel (4), s. 525) som enklast formuleras m.hj.a. räkneregeln i2 = -1 tillsammans med de vanliga reglerna som gäller för reella tal. Egenskaper och begrepp Komplext tal (def. s. 522) Real- och imaginärdel (s.523) Addition (s.524) och multiplikation (s. 525) av komplexa tal. Kom ihåg i2 = -1. Hemuppgifter 6b 9b 14 17

10.2  Modulus; Complex Conjugate; Division

Avsnittet börjar med att definiera begreppet konjugat: Om z =a + bi definieras z-konjugatet: 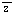= a - bi. Konjugering innebär alltså spegling i den reella axeln (x-axeln). Beloppet (Modulus) av ett komplext tal z = a + bi är: |z| = (a2 + b2)1/2 Beloppet är alltså lika med normen av motsvarande 2-dimensionella vektor (a,b). Thm 10.2.2 formulerar den viktiga egenskapen (som gör de komplexa talen till ett fungerande talsystem) att om z 0 så finns ett unikt komplext tal w som är invers till z, dvs. zw = 1. Division (utom med 0) är alltså tillåten. Det finns ett visst knep (förlängning med konjugatet) som används för att skriva om kvoter av komplexa tal till normalformen a + bi. Detta visas i Ex. 3, s.531, och bör studeras. I Thm 10.2.3 anges några räkneregler för z-konjugat. Egenskaper och begrepp = a - bi, z-konjugat, (s.528) Beloppet |z| av z (Modulus, s. 529). Varje komplext z0 har en unik komplex invers (Thm 10.2.2 ,s.530). Knepet att bli av med 'i' i nämnaren (ex.3 s.531) Regler för . Hemuppgifter 1bde 2bde 4bc 11 14

10.3   Polar Form; DeMoivre's Theorem

Här införs den viktiga polära formen för komplexa tal: z = r(cos + i sin) Detta skrivs ofta på exponentialform: z = ei     (12), s. 542 Den polära formen ger den bästa geometriska tolkningen av komplex multiplikation. Studera gärna Ex. 2 på s. 538 där multiplikation och division studeras m.hj.a. övergång till polär form. DeMoivre's formel visar hur potensuttryck som zn lätt kan återföras på normalform. Avslutningsvis visas hur man löser s.k. binomiska ekvationer: zn = w0 (z variabel, w0 konstant komplext tal). Det visar sig att rötterna till sådana ekvationer alltid bildar regelbundna n-hörningar i det komplexa planet. Egenskaper och begrepp Polär form, s. 536 DeMoivre's formel, s. 539 Binomiska ekvationer och deras lösning, s. 540+Ex.3,4 s. 541 Hemuppgifter 3df 4cd 6b 11a 12