Ola Henrikssons lösning av den grekiska extranöten.

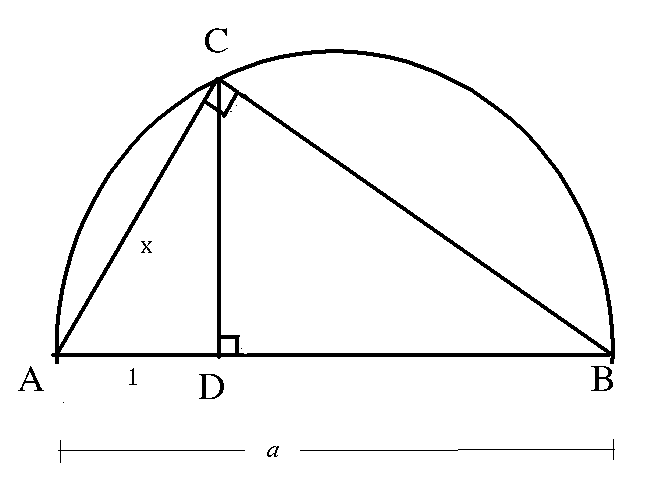
Konstruera triangeln ABC genom att

• låta a vara längden av diametern AB i en cirkel.
• låta D vara en punkt på AB med avståndet 1 från A (antag 1 < a).
• Dra en linje genom D vinkelrätt mot AB. C är den punkt där denna linje skär cirkeln.

Man ser nu att trianglarna ABC och ADC (samt även DBC) är likformiga.
Båda har en rät vinkel och dessutom är en vinkel gemensam.

Antag att sträckan AC har längden x.

Då gäller p.g.a. likformogheten att

x/1 = a/x

vilket ger att x² = a , dvs x är den sökta sträckan!

(Om a < 1 kan man låta a och 1 byta roller i konstruktionen.)