|
Institutionen för Matematik, KTH
5B1102/1, Differential- och integralkalkyl I, del 2Läsanvisningar till R.A. Adams, Calculus, a Complete Course, 4th ed.[Detta är de officiella läsanvisningarna gemensamma för alla linjer som läser B1102/2.] Omfattning:
| |||||||||||||||||||
| Kedjeregelexempel 1
Kedjeregelexempel 2 |
I. Derivator och integraler i flera variablerKapitel 12. Partiella derivator12.1 Funktioner av flera variabler.
12.2 Gränsvärden och kontinuitet i flera variabler.
12.3 Partiella derivator.
12.4 Högre partiella derivator. 12.5 Kedjeregeln. | ||||||||||||||||||
|
Normalvektor och riktningsderivata |
12.6 Linjär approximation mm. 12.7 Gradient och riktningsderivata.
12.8 Implicita funktioner. 12.9 Taylors formel mm.
| ||||||||||||||||||
Kapitel 13 Tillämpningar av partiella derivator13.1 Extremvärden.
Th. 1 visar att extremvärden bestäms ungefär som i en dimension, men det är mer krävande. Man måste kolla fler derivator och analysen av en funktion på randen, en eller flera kurvor i två dimensioner, är förstås besvärligare. 13.2 Största och minsta värden. 13.3 Lagrangemultiplikatorer | |||||||||||||||||||
|
Dubbelintegral 1 Dubbelintegral 2 |
Kapitel 14. Multipelintegraler14.1 Dubbelintegraler. 14.2 Dubbelintegraler och upprepad integration. 14.3 Generaliserade dubbelintegraler och upprepad integration. 14.4 Dubbelintegraler i polära koordinater.
Ex 7-8.
14.5 Trippelintegraler.
Trippelintegraler införs och beräknas helt analogt med dubbelintegraler.
Denna gång fås volymen vid integration av funktionen 1.
14.6 Variabelbyte i trippelintegraler. Helt analogt med avsnitt 14.4. Notera speciellt cylindriska koordinater (polära koordinater tillsammans med z), sid 856-857,
Ex 2-3. 14.7 Tillämpningar av multipelintegraler.
Observera att ytelementet dS (sid 865) är helt analogt med
båglängdselementet i en variabel. I stället för
II. VektoranalysKapitel 8 och 11 i urval; Kurvor, båglängd mmTanken är att parallellt läsa om kurvor i två (Kap. 8) och tre (Kap. 11) dimensioner. (8.1 Orientering om andragradskurvor som "kägelsnitt" för de intresserade.) 8.2-8.3 t.o.m. sid 497.Dessa avsnitt är av orienterande karaktär. Man skall främst lära sig att handskas med kurvor med allmän parameter. 8.2 Parametrisk kurva, def. 4. 8.3 Sats 1, Ex. 1-2. Tangent och normal till plana kurvor.
8.4 tom sid 501. Båglängdsformeln, sid 500. Dess förklaring i fig. 8.28 (Pythagoras sats).
8.5 Polära koordinater (igen), sid. 506.
11.1 Viktiga begrepp: position, hastighet (velocity) och acceleration för en
kurva (sid. 646-648).
11.3 Det är viktigt att förstå att en kurvas hastighet och fart osv
beror på parametriseringen. Man kan genomlöpa en viss kurva olika snabbt.
Kapitel 15 Vektorfält(15.1 Detta avsnitt, som handlar om vektorfält, är snarast en orientering inför senare studier av linje- och flödesintegraler. Läs gärna t.o.m. sid 879.)
15.2 t.o.m. sid 887. Begreppen konservativt fält och potentialfunktion är viktiga (Def. 1). 15.3 Läs Ex. 1-2 som exempel på hur man integrerar funktioner m.a.p. båglängd. En tolkning av detta är arean av ett staket, där C är basen (tomtgränsen), och f höjden av staketet.
15.4 Linjeintegralen motiveras genom arbete = kraft . sträcka. Dess
definition
och olika sätt att skriva integralen framgår av rutan på sid. 897.
15.5 Vi skall bara behandla integraler över funktionsytor (grafer).
15.6 Normal, orientering: se fig. 15.26. Flöde (flödesintegral): Kapitel 16 Integralformler16.1 till mitt på sid 929.Divergens och rotation (curl):övre rutan på sid 928. Gradienten, sid 927, känner vi till sedan tidigare. Det är viktigt att göra klart för sig hur operationerna fungerar: grad är definierad för funktioner och ger vektorer. div är definierad för vektorer och ger funktioner (skalärer), medan rotationen är definierad för vektorer och ger vektorer. Läs Ex. 1-2.
16.3 Huvudresultatet är Greens formel, Th. 6.
16.4 Det viktiga resultatet är divergenssatsen, Gauss' formel, i Th. 8.
(16.5 Stokes' sats är helt enkelt Greens formel för en krökt yta.)
8.2 : 1, 9, 15.
|
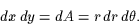
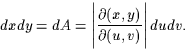
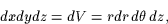
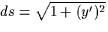 dx har vi nu
dx har vi nu 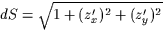 dxdy .
dxdy .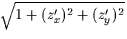 är längden av den
(onormaliserade) normalvektorn till ytan,
är längden av den
(onormaliserade) normalvektorn till ytan, 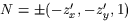 .
.