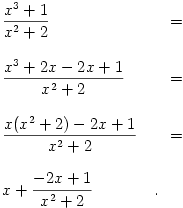KTHs Sommarmatematik 2003 2.3 Exempel

Exempel 1

Kvadratkomplettera:

Exempel 1

Bryt först ut koefficienten för x2,
här 3.

x-termen (5/3)x skall nu vara den blivande kvadratens dubbla produkt.

Därför blir kvadraten (x + 5/6)2.

Slutligen måste man dra ifrån (5/6)2 och förenkla konstanttermen för att det hela skall stämma. 


 

 Exempel 2 







Kvadratkomplettera:

Exempel 2


 
 
 
 Bryt ut x2-koefficienten 4.

Identifiera dubbla produkten, 3a/2, och bilda kvadraten,

 (x + 3a/4)2.

Slutligen dras kvadraten (3a/4)2 ifrån 

och uttrycket snyggas till.

Observera förekomsten av parametern a, som dock inte förändrar
principen.





















 

 Exempel 3 







Kvadratkomplettera:

Exempel 3


 

 Samma procedur som förut, trots tre parametrar:
 
p bryts ut, (4q/p)x är dubbel produkt.
 
Kvadraten blir (x + 2q/p)2
 
Konstanttermen snyggas till så gott det går.












 

 Exempel 4 







Lös följande andragradsekvation:

Exempel 4






Dividera ekvationen med 2 för att återföra
den till normalform.

Använd sedan lösningsformeln.




















 

 Exempel 5 







Lös följande andragradsekvation::

Exempel 5






Här kan man naturligtvis också använda lösningsformeln (med p=0 )

Men i detta enkla fall är faktorisering med konjugatregeln 

a2 - b2 = (a+b)(a-b)

naturligast.











 










 

 Exempel 6 







Lös följande andragradsekvation:

Exempel 6






Efter division med 3 och användande av lösningsformeln får
man ett negativt tal under rottecknet, vilket visar att lösning saknas.

Samma resultat ger kvadratkomplettering:

3(x2 + (4/3)x + 7/3) = 

3((x+2/3)2 -4/9 + 7/3)=

3((x+2/3)2 + 17/9).

Kvadratkompletteringen visar att uttrycket alltid är > 0
och alltså inte har några nollställen.









 

 Exempel 7 







Utför följande polynomdivision:

Exempel 4






 Här visas direktdivision av polynom, där alla beräkningar
 utförs i anslutning till det givna bråkstrecket.
 
En annan metod som svarar mot 'liggande stolen' för
 numerisk division visas i avsnittets SfS-exempel.

  Metoden här bygger på att man i täljaren skapar en multipel av nämnaren. Där skall täljarens  högstagradsterm  ingå  (här x3).

 Man ser att
x3 + 2x behövs för att skapa en multipel av x2 + 2.

Därför lägger man till och drar ifrån 2x i täljaren.

Efter dessa förberedelser är det bara att skriva ut resultatet.

Notera att (x2 + 2) förkortas bort så att kvoten x erhålles.

Man är färdig då den erhållna resten, här -2x +1, har lägre gradtal
än nämnaren.










 



 
 
  
  
  
 
  
  		 
  
   	  
	 


 



	 

 	 	

   		 
    			

    			

    			

    					
		

      		

      	 
  	  Avdelning Matematik
   		
   		  Matematik KTH