qint2.html

Integration av en rationell funktion.

Vi studerar här partialbråksutveckling och integrering av en konkret
rationell funktion, Z(x).
Avsikten är att ge förtrogenhet med partialbråksutveckling och hantering av de logaritmer som uppkommer efter integrationen.

> restart;

> Z := (x^2+2)/((x^2-4*x+1)*(x^2+1));

[Maple Math]

Maple har ett kommando som utför partialbråksutveckling.
Vi prövar det på Z(x):

> Z1:=convert(Z,parfrac,x);

[Maple Math]

Maple utförde en viss partialbråksutveckling, men upptäckte inte
att första termen kan partialbråksutvecklas ytterligare efter faktorisering
av nämnaren.
Vi försöker en gång till:

> Z2:=convert(Z1,parfrac,x);

[Maple Math]

Nej, Maple klarar inte av den faktoriseringen.
Det finns dock ett sätt att hjälpa Maple här.
Om man räknar för hand för att faktorisera nämnaren
upptäcker man att nämnarens nollställen innehåller
det irrationella talet 'roten ur 3'.
Den informationen visar sig Maple behöva:

> Z1:=convert(Z,parfrac,x,sqrt(3));

[Maple Math]

Här lyckades den reella partialbråksutvecklingen.
Vi låter nu Maple integrera Z(x) och dess partialbråksutvecklade
version Z1(x) för att se om det blir någon skillnad:

> W1:=int(Z,x);
W2:=int(Z1,x);

Man ser här att Maple tänker olika vid integreringen av Z och Z1.
I det förra fallet används funktionen arctanh som är inversen till tanh,
som definieras av tanh(x) = sinh(x)/cosh(x).
Ett speciellt drag hos Maple är att integralerna av 1/(x+a) alltid skrivs
som en logaritm utan absolutbeloppstecken, ln(x+a). Detta skulle kunna vara
en källa till fel, ex.vis vid integration av uttrycken ovan mellan 1 och 2.
Man ser att vid insättning av dessa gränser får ln-termer i W1 negativa argument.
Maple tycks dock kunna hantera detta vilket man ser vid beräkningen av
motsvarande bestämda integraler mellan 1 och 2:

> Q1:=int(Z,x=1..2);
Q2:=int(Z1,x=1..2);

Här har alla negativa argument försvunnit.

Man bör dock tänka på Maples frånvarande absolutbelopp
då man använder de obestämda intehgralerna för vidare kalkyler.
Vi avslutar med att evaluera de båda uttrycken numeriskt
för att kontrollera att vi fått samma värde:

> q1:=evalf(Q1);
q2:=evalf(Q2);

Samma negativa värde (åtminstone fram till tionde decimalen).
Detta visar dock att de båda primitiva funktionerna bör vara identiska.
Vi avslutar med att plotta kurvan y = Z(x)
för att se om kurvan ligger under y-axeln i intervallet [1,2]:

> plot(Z,x=0..6,y=-4..4);

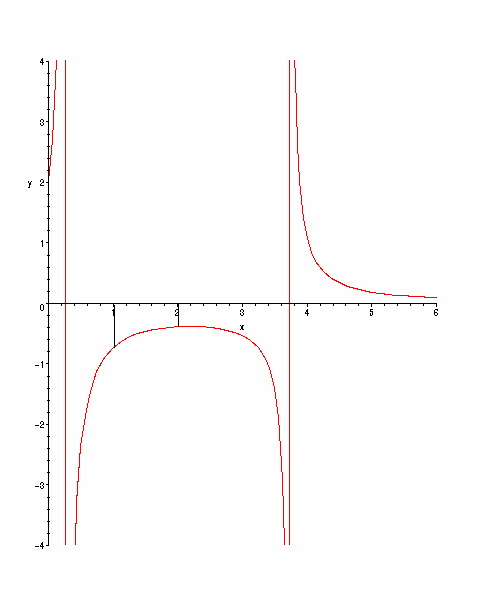
Av plotten framgår det att kurvan antar negativa värden i
intervallet [1,2], vilket motiverar det negativa värdet för
integralen.