3-dimensionell plottning kan göras i Maple med kommandona

'plot3d' och 'implicitplot3d'.

Man måste då först ladda in paketet 'plots'.

Skriv alltså 'with(plots):' efter 'restart'.

Som vanligt med paket undviker man stor output genom

':' efter i stället för';'..

> restart;

> with(plots):
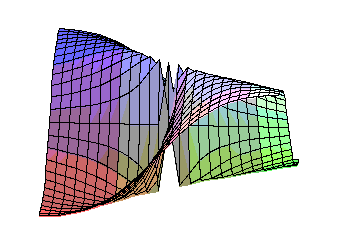
Vi definierar nu en av de vanligaste spiraltrappsytorna för att om möjligt kunna
studera utseendet nära origo.:

> f:=x*y/(x^2+y^2);

Plottningskommandot är enklast tänkbara:

>
plot3d(f,x=-1..1,y=-1..1);

Lägg märke till att man kan vrida och vända på denna graf (i Maple)..

Klicka på plotten så att en ram framträder.

Enkelklicka en gång till innanför ramen så framträder istället en låda (man kan behöva försöka några gånger).

Denna låda kan vridas med visaren (nedtryckt mustangent).

Dubbelklicka på lådan så framträder grafen igen i ett nytt perspektiv svarande mot lådans nya läge.

Om man behöver ange ett intervall i z-led så gör man det med 'view=a..b' inne i plot3d-funktionen:

> plot3d(x^2+y^2, x=-2..2,y=-2..2,view=0..4);

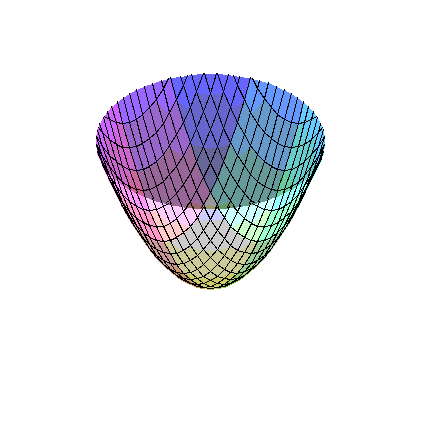
Här prövar vi implicitplot3d med en funktion som innehåller parameterna a och b.
med olika värden på a och b erhålles ellipsoider samt en- och tvåmantlade hyperboloider.

Med valen här får man en enmantlig hyperboloid:

> a:=1;
b:=-1/4;
g:=x^2+a*y^2+b*z^2-1;f := x*y/(x^2+y^2);

Lägg märke till att man anger z-intervallet med ' z=-2..3 ' här.
I stället för 'g' kan man skriva ' g=0' vilket ger samma plot.

> implicitplot3d(g ,x=-2..2,y=-2..2 ,z=-2..3);

Kör gärna det här i Maple och pröva med flera värden på a och b!

Slutligen visar vi hur man kan plotta flera ytor samtidigt.
Vi lägger in planet y=1, som tangerar hyperboloiden.

Därvid används, som för vanliga plot-funktionen, en klammerparentes omkring de två ekvationerna:

> implicitplot3d({g=0,y=1} ,x=-2..2,y=-2..2 ,z=-2..3);

>