cos(u-v) = cosu cos v + sin u sin v
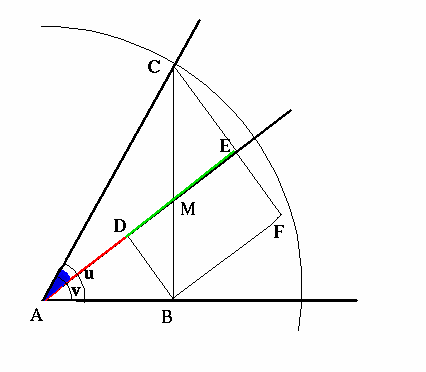
|
kan ges ett geometriskt bevis.
Vi antar först att u och v ligger mellan 0 och pi/2 och att u > v.
Då fungerar figuren här till vänster.
Antag att cirkeln har radien = 1.
Man ser då att cos(u-v) [vinkeln u-v är märkt med blå färg] ges av sträckan
AE, som i sin tur utgör summan av sträckorna
AD[ röd ] och DE [ grön ].
Vi skall visa att AD = cos u cos v
och att DE = sin u sin v.
AD:
Observera att AB = cos u och att AD = AB cos v,
dvs AD = cos u cos v.
DE:
Observera att BC = sin u.
Dessutom är vinkeln BCF = v,
eftersom ABM och CME är likformiga
(de är båda rätvinkliga
och vinkeln CME = vinkeln AMB).
Därför:
DE = BF = BC·sin v = sin u sin v.
Formeln kan också visas gälla för andra än spetsiga vinklar.
VSB