Introduction
This page describes in general terms the area in which I see the prospective PhD student working in.
Random conformal geometry
Random Conformal Geometry is a field at the intersection of probability, complex analysis, geometry, and mathematical physics. Basic questions come from trying to understand in a precise mathematical way scaling limits of various models from statistical physics such as the Ising model and percolation at criticality. Such scaling limits turn out to exhibit very interesting universal (i.e., one sees them in many seemingly different places) geometric, fractal structures which have been the subject of intense mathematical research activity in recent years.
Tools such as the SLEs, discrete complex analysis, and Gaussian random fields have led to impressive progress on several fronts. Still, there are many fundamental things to understand.
For example, we would like to understand the precise analytic and probabilistic content of the powerful (and mysterious!) but non-rigorous Conformal Field Theories used by physicists to study conformally invariant systems.
A very interesting and (very) recent development is the Loewner energy which connects many of the central themes in this story and is further linked with Teichmueller theory and other exciting new points of view.
For the advertised PhD positions we have in mind project(s) that go in one or several of these directions, in particular towards Loewner energy. We encourage applicants with a strong background either in complex analysis or probability (or both!) Please get in touch (frejo - at - kth.se) for more information.
References
Popular science article on some aspects of my work:
https://kaw.wallenberg.org/en/research/using-new-mathematics-explain-natures-random-patterns
Popular science article by my collaborator Amanda Turner (in part) on our joint work with Alan Sola:
https://www.lms.ac.uk/sites/lms.ac.uk/files/files/NLMS_482_reduced.pdf
Popular science article on the work of Jason Miller and Scott Sheffield:
https://www.quantamagazine.org/a-unified-theory-of-randomness-20160802/
Key players:
https://en.wikipedia.org/wiki/Schramm%E2%80%93Loewner_evolution
https://en.wikipedia.org/wiki/Gaussian_free_field
https://en.wikipedia.org/wiki/Conformal_field_theory
Loewner energy:
https://arxiv.org/abs/1802.01999
https://arxiv.org/abs/1903.08525
https://arxiv.org/abs/2012.05771
Understanding CFT:
https://arxiv.org/abs/1307.4104
https://arxiv.org/abs/1701.03698
Rough conformal welding
https://projecteuclid.org/euclid.acta/1485892580
http://sites.math.washington.edu/~rohde/papers/conformal%20welding%20of%20dendrites.pdf
Simulations
Below are a few samples of objects that one can encounter in random conformal geometry....
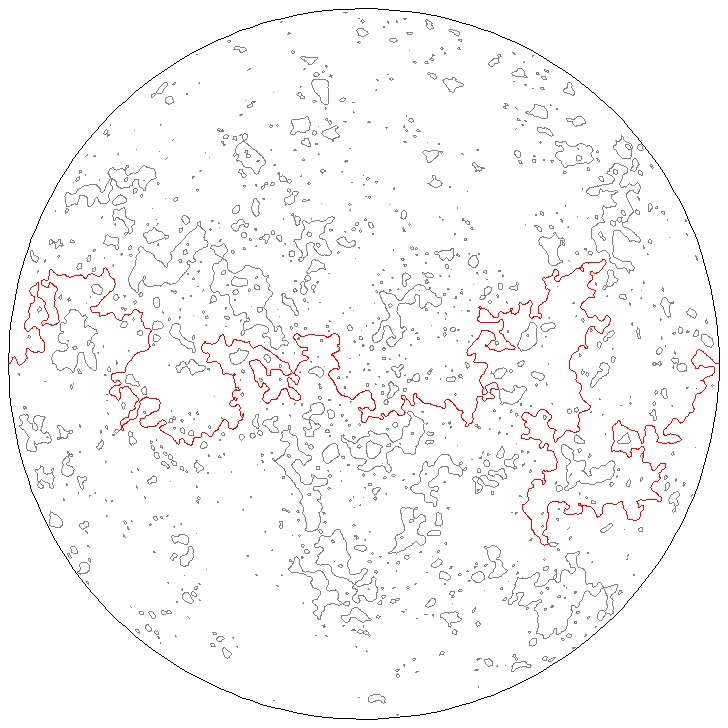
[A dicrete Gaussian free field with a level line. Image by Nam-Gyu Kang]
[A regularized Hastings-Levitov cluster. From joint work with Alan Sola and Amanda Turner]
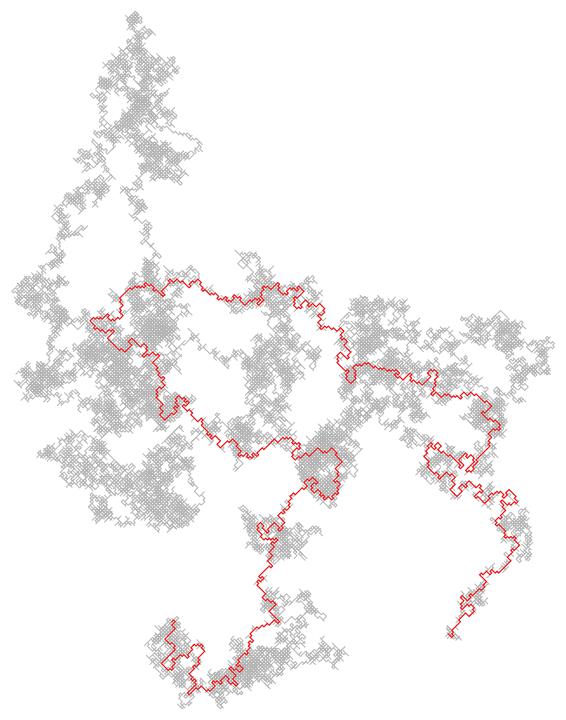
[A loop-erased random walk path with the `parent' random walk drawn in grey. The LERW is obtained by erasing the loops chronologically from a simple random walk. In the scaling limit, the LERW path converges to an SLE(2) curve.]
[Image by Jason Miller]
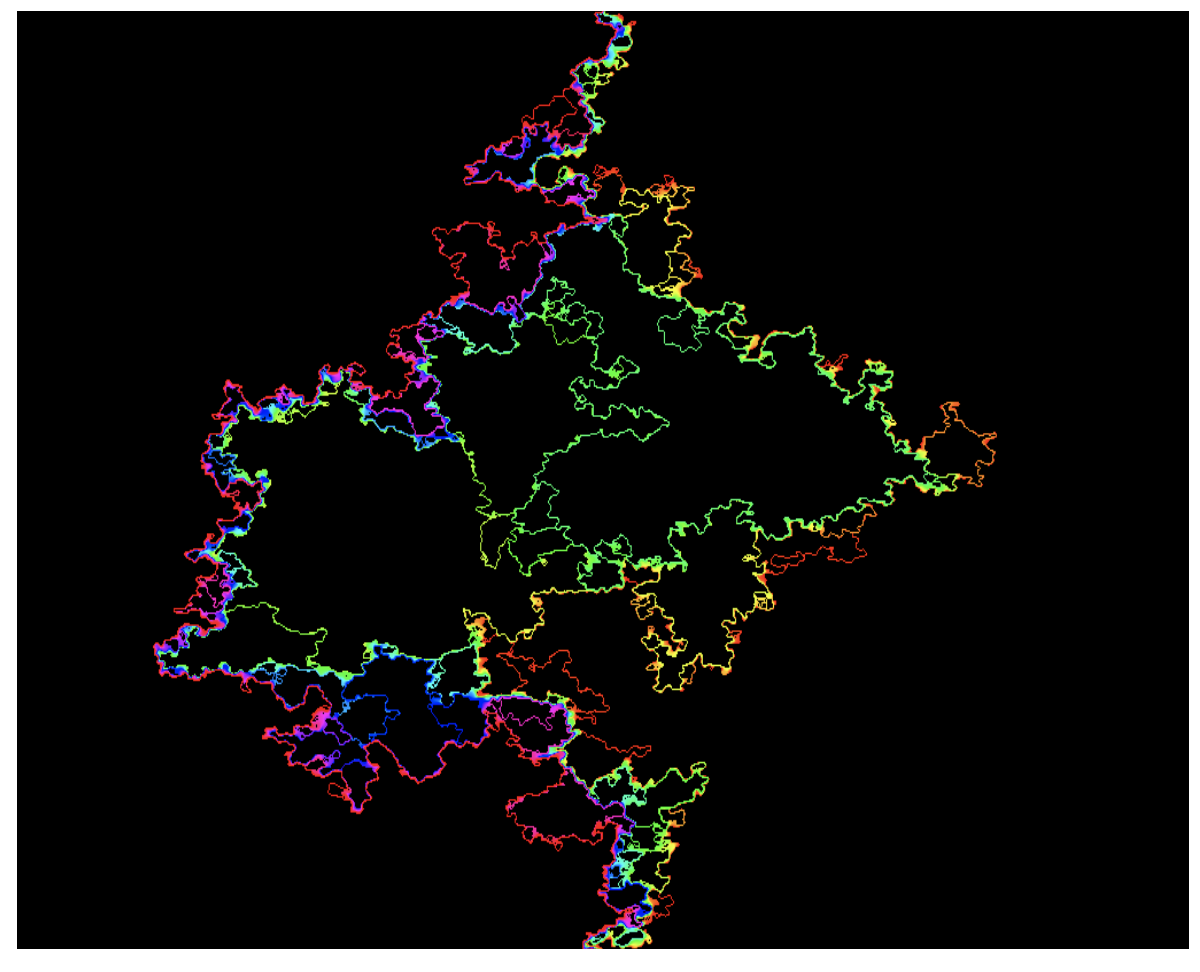
[`Flow lines' of a GFF; they are different SLE curves that are deterministic functions of the underlying Gaussian field. Image by Jason Miller]
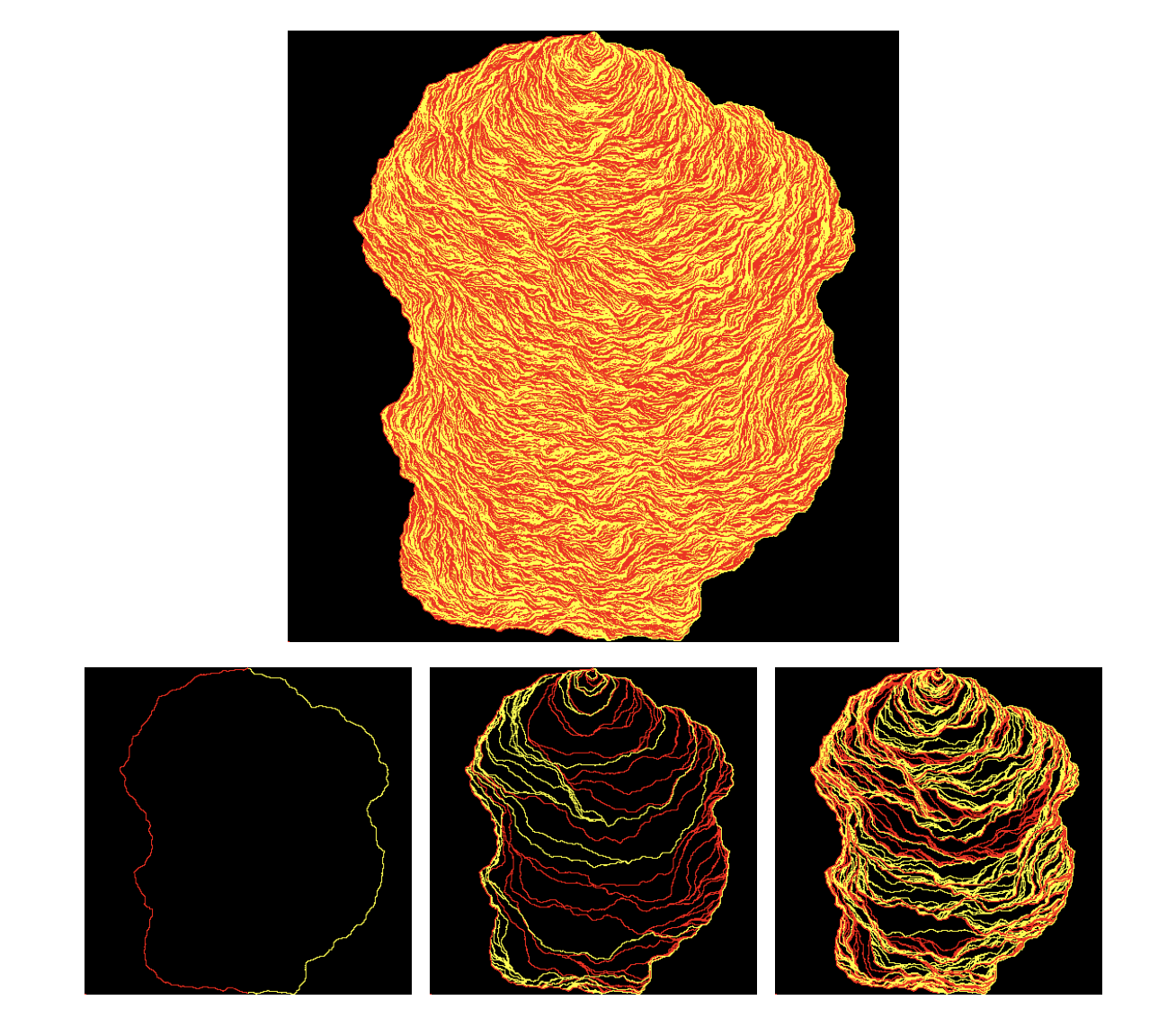[Image by Jason Miller]