Maximum Period NLFSRs

Below we give a complete list of n-bit NLFSRs with the period 2ⁿ−1, n < 26, for the following types of feedback functions:

₀

where "⊕" is an XOR (addition modulo 2) and " · " is an AND.

The maximum possible period for a n-bit NLFSR is 2ⁿ. The NLFSRs listed below do not include all-0 state in their longest cycle of states. They can be extended to have the period 2ⁿ by adding to their feedback function a product-term ¬x₁ · ¬x₂ · ... · ¬x_n−1, where "¬" is a NOT. This increases the circuit complexity of feedback functions, which is undesirable for many applications. For this reason, we prefer to focus on NLFSRs with the period 2ⁿ−1.

The results given below were computed by a brute-force simulation which feasible for n < 26 only. FPGAs make possible finding larger maximum period NLFSRs, as shown in this article.

INTRODUCTION TO NLFSRs

The general structure of an n-bit NLFSR is shown in Figure 1. It consists of n binary storage elements, called bits or stages, and a feedback function f(x₀,x₁,...x_n−1). For each i ∈ {0,1,...,n−1 }, the state variable x_i represents the value of the bit i. At each clock cycle, the content of the register is shifted one bit right. The value of the bit n−1 is updated according to the feedback function f.

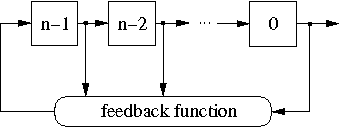
Figure 1: The general structure of an n-bit NLFSR.
The configuration shown in Figure 1 is usually referred to as the Fibonacci configuration. One can also represent an NLFSR in the Galois configuration, in which any stage has its own feedback function.

Figure 2 shows an example of a 4-bit NLFSR with the feedback function f = x₀ ⊕ x₁ ⊕ x₂ ⊕ x₁· x₂.

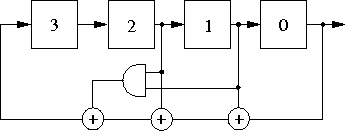
Figure 2: An example of a 4-bit NLFSR

FORMAT OF FEEDBACK FUNCTIONS

In the format we use in the list below, the function f = x₀ ⊕ x₁ ⊕ x₂ ⊕ x₁· x₂ from the example in Figure 2 is represented as 0,1,2,(1,2). Indexes of variables of each product-term are separated by a comma. If a product-term has of more than one variable, we put round brackets around the indexes of its variables.

BASIC AND IMPLIED CASES

The state transition graph of an n-bit NLFSR is branchless, i.e. consists of pure cycles, if and only if its feedback function is of type

₀

₁

₂

_n−1

where the function g(x₁,x₂,...,x_n−1) does not depend on the variable x₀.

Each NLFSR N with the feedback function of type (1) has a revserse, a complement, and a reverse-complement NLFSRs which generate sequences which are reverse, complement and reverse-complement of sequences generated by N, respectively. In the list below, we show only the basic case. Other three cases are not included.