Facit till rekommenderade uppgifter vecka 4
- 13.1.1
- Addition har alla fyra egenskaper, subtraktion har alla utom associativitet och multiplikation har alla utom invers. (Svar finns i Biggs.)
- 13.2.4
| |
1 |
-1 |
i |
-i |
| 1 |
1 |
-1 |
i |
-i |
| -1 |
-1 |
1 |
-i |
i |
| i |
i |
-i |
-1 |
1 |
| -i |
-i |
i |
1 |
-1 |
- 13.3.1
- b-1 a-1ab=b-1 (a-1a )b=b-1 (e)b=b-1 b=e, och
abb-1 a-1=a(bb-1 )a-1= aea-1=aa-1=e.
- 13.3.3
- Vi vill visa att ab=ba för alla a och b i G. Eftersom a2=e är a-1=1 för alla a i G. Vi har därför att (ab)-1=(ab), och enligt den tidigare uppgiften är (ab)-1=b-1a-1=ba. Därmed är ab=ba för alla a och b i G.
- 13.4.1
- Ordningen av a är 10 och ordningen av b är 4. ab och ba har båda ordning 6.
- 13.5.1
- Genom att låta a vara rotation ett halft varv och b och c vara speglingar parallellt med kanterna får vi grupptabellen
| |
1 |
a |
b |
c |
| 1 |
1 |
a |
b |
c |
| a |
a |
1 |
c |
b |
| b |
b |
c |
1 |
a |
| c |
c |
b |
a |
1 |
vilken överenstämmer med den angivna tabellen. Alltså är grupperna isomorfa. För att se att det måste bli just denna tabell räcker det med att se att alla element är sina egna inverser och att 1 är identitetselementet. Resten av tabellen kan fyllas i genom att tabellen skall vara en latinsk kvadrat.
- 13.5.2
- Enligt samma princip som i uppgiften innan kan vi med hjälp av att det finns en enhet och en invers till varje element sluta oss till att grupptabellen för 2 element {e,a}
eller för 3 element {e,a,b}
bara kan se ut på ett sätt, medan det finns två möjliheter för grupptabellen för fyra element {e,a,b,c}.
- 13.6.1
- Genom att hitta ett element av ordning 6 kan vi ge en isomorfi från U till C6. Vi prövar elementen i tur och ordning och ser att o(1)=1, o(2)=3, o(3)=6. Därmed kan 3 väljas till generator, 31=3, 32=2, 33=6, 34=4, 35=5, 36=1.
- 13.6.4
- Det räcker att se att grupptabellerna är lika. Eftersom det bara finns två möjliga grupptabeller räcker det att se att det i den ena finns ett element av ordning 4, och att alla element i den andra är sina egna inverser.
- 13.7.1
- K1 är en delgrupp, men inte K2 eller K3. K1 är isomorf med C2, medan varken K2 eller K3 är slutna under sammansättning, exempelvis är xy=s och ry=z.
- 13.7.3
- Om ab ligger både i H och K ligger ab i
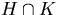 . Därmed är . Därmed är 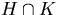 sluten under samma gruppoperation som G. På samma sätt ligger a-1 i sluten under samma gruppoperation som G. På samma sätt ligger a-1 i 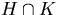 om den ligger i både H och K och om den ligger i både H och K och 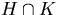 är sluten under invers. Detta räcker för att är sluten under invers. Detta räcker för att 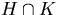 skall vara en delgrupp. skall vara en delgrupp.
- 13.8.2
- Vänstersidoklasserna av {i,x}
i triangelgruppen är {y,yx}={y,r}, {z,zx}={z,s}
och {i,x}.
Högersidoklasserna av {i,x}
i triangelgruppen är {y,xy}={y,s}, {z,xz}={z,r}
och {i,x}.
Dessa partitioner är inte lika.
- 13.10.8
- Gruppen genereras av
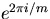 ,
och vi får en isomorfi genom ,
och vi får en isomorfi genom 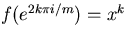 , för k=0,1,2,...,m, om x är generatorn för Cm. , för k=0,1,2,...,m, om x är generatorn för Cm.
- 15.2.1
-
U(Z10)={1,3,7,9} är isomorf med C4 och har ordning 4. (3 är en generator.)
U(Z11)={1,2,3,4,5,6,7,8,9,10} är isomorf med C10 och har ordning 10. (2 är en generator.)
U(Z12)={1,5,7,11} är isomorf med
C2xC2
och har ordning 4.(Alla element är sina egna inverser.)
- 15.2.3
- De gaussiska heltalen är slutna under addition och multiplikation. De är en abelsk delgrupp av de komplexa talen under addition och de uppfyller associativa lagen för multiplikation eftersom de är en delmängd av de komplexa talen. Likaså är de distibutiva lagarna uppfyllda eftersom de är uppfyllda för de komplexa talen.
De inverterbara elementen är 1,-1,i,-i och den multiplikativa gruppen är isomorf med C4 med i som generator.
- 15.3.2
- 5, 7, 10, 11, 14, 15, 17, 19, 20, 21 är möjliga generatorer.
- 15.4.1
- (i) x5+2x4+x3+3x+2. (ii) x7+x4+x3+x2+3x+2.
- 15.4.3
- 15.4.4
- Eftersom alla binomialkoefficienter i utvecklingen av (1+x)7 utom den första och den sista är delbara med 7 så får vi (1+x)7=1+x7.
I allmänhet gäller att (1+x)m=1+xm om och endast om m är ett primtal.
- 15.5.1
- x+1.
- 15.6.1
- 2,x+1.
- x+4.
- 15.6.3
- (i) x2+1. (ii) x+1. (iii) x3+1. I allmänhet är det xd+1 där d=sgd(m,n).
- 15.7.6
- (x+1)(x+14)=x2+14=(x+4)(x+11) i Z15[x].
Det visar att det är ett nödvändigt krav att koefficienterna tillhör en kropp för att det skall vara unik faktorisering i polynomringen.
- 15.7.3
- Skriv 1=p(x)r(x)+q(x)s(x). Multiplicera detta med t(x), så får vi t(x)=p(x)r(x)+q(x)s(x)t(x) och om r(x) delar s(x)t(x) delar r(x) båda termerna i summan, varför t(x) är delbart med r(x).
- 15.8.1
- (i) x2+1=(x+2)(x+3) i
Z5[x].
(ii) x3+5x2+5=(x+8)(x+9)(x+10) i Z11[x].
(iii) x4+3x3+x+1=(x2+2)(x2+3x+3) i Z5[x].
- 15.8.2
- x2+1, x2+x+2 och x2+2x+2.
- 15.9.1
- C2xC4
i båda fallen.
- 15.9.2
- (i) x4+4=(x+1)(x+2)(x+3)(x+4) i Z5[x]. (ii) x4+3x3+2x+4=(x+1)(x+4)3 i Z5[x].
- 15.9.5
- x2+2x+1 respektive x2+6x+1.
- 15.9.17
- Det räcker att se att mängden är sluten under addition och multiplikation och additiv invers eftersom det är en delmängd av de reella talen som bildar en ring. När vi multiplicerar två element
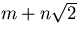 och och 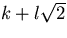 multipliceras deras normer m2-2n2 och k2-2l2. Om resultatet skall bli 1, måste produkten av normerna också vara 1, och vi får att multipliceras deras normer m2-2n2 och k2-2l2. Om resultatet skall bli 1, måste produkten av normerna också vara 1, och vi får att 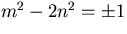 för att för att 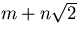 skall vara inverterbart. Å andra sidan är inversen lika med skall vara inverterbart. Å andra sidan är inversen lika med 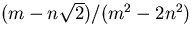 , vilket ligger i mängden om m2-2n2 är ett inverterbart heltal, dvs , vilket ligger i mängden om m2-2n2 är ett inverterbart heltal, dvs 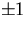 . .
|
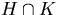 . Därmed är
. Därmed är 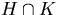 sluten under samma gruppoperation som G. På samma sätt ligger a-1 i
sluten under samma gruppoperation som G. På samma sätt ligger a-1 i 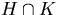 om den ligger i både H och K och
om den ligger i både H och K och 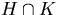 är sluten under invers. Detta räcker för att
är sluten under invers. Detta räcker för att 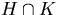 skall vara en delgrupp.
skall vara en delgrupp.
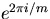 ,
och vi får en isomorfi genom
,
och vi får en isomorfi genom 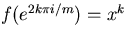 , för k=0,1,2,...,m, om x är generatorn för Cm.
, för k=0,1,2,...,m, om x är generatorn för Cm.
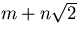 och
och 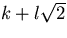 multipliceras deras normer m2-2n2 och k2-2l2. Om resultatet skall bli 1, måste produkten av normerna också vara 1, och vi får att
multipliceras deras normer m2-2n2 och k2-2l2. Om resultatet skall bli 1, måste produkten av normerna också vara 1, och vi får att 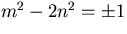 för att
för att 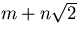 skall vara inverterbart. Å andra sidan är inversen lika med
skall vara inverterbart. Å andra sidan är inversen lika med 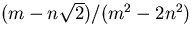 , vilket ligger i mängden om m2-2n2 är ett inverterbart heltal, dvs
, vilket ligger i mängden om m2-2n2 är ett inverterbart heltal, dvs 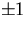 .
.