| Institutionen för matematik KTH |
| Avdelningen för matematik 5B1118 Diskret matematik |
| IT | 5B1118 Diskret matematik | HT01 |
Facit till rekommenderade uppgifter vecka 2
- 3.1.1
- 49. (Finns svar i Biggs.)
- 3.1.2
- Mängderna av multipler av två respektive multipler av tre är inte disjunkta mängder, så additionsprincipen kan inte användas.
- 3.1.4
- Antag att det inte finns tre personer som alla inte känner varandra. Enligt exemplet i avsnitt 3.1 finns det då i varje uppsättning av sex personer tre som alla känner varandra. Välj nu en person A bland de tio personerna.
Om A känner färre än sex andra finns det fyra personer den inte känner. Om det bland dessa fyra finns två, B och C, som inte känner varandra ger trippeln {A,B,C} en motsägelse mot antagandet. Alltså måste alla fyra känna varandra, och det finns i så fall fyra personer där alla känner alla.
Om A känner minst sex andra finns bland dem tre där alla känner alla och då bildar A tillsammans med dessa en grupp om fyra där alla känner alla.
Vi har nu visat att om det inte finns tre personer som inte känner varandra alls, så finns det fyra där alla känner alla.
- 3.2.1
- 20. (Finns svar i Biggs.)
- 3.2.5
- 264, 254. (Finns svar i Biggs.)
- 3.3.1
- 18, 8, 12. (Finns svar i Biggs.)
- 3.3.3
- Eftersom n=pm endast har ett primtal som delar n, nämligen p, så måste ett heltal som x som har en gemensam faktor med n vara delbart med p. Det finns pm-1 heltal mellan 1 och pm som är delbara med p, nämligen kp för k=1,2,...,pm. Alltså måste resterande pm-pm-1 tal mellan 1 och pm vara relativt prima med pm och därmed är fi(pm= pm-pm-1.
- 3.4.1
- 43=64. (Finns svar i Biggs.)
- 3.5.1
- 14 529 715 200 (Finns svar i Biggs.)
- 3.5.4
- Om vi utan återläggning men med ordning skall välja ut r element från en mängd med n element kan vi dela upp det i två steg. Först väljer vi utan återläggning och med ordning ut m element. Sedan väljer vi utan återläggning men med ordning ut r-m element bland de återstående n-m elementen. Vi kan välja de första m elementen på [n]m sätt. Eftersom vi för varje val av de m första har [n-m]r-m möjliga val för de återstående r-m måste vi ha [n]r= [n]m [n-m]r-m.
- 3.6.1
- (137)(2548)(6)(9). (Finns svar i Biggs.)
- 3.6.2
- st=(1)(24587)(36), ts=(16478)(25)(3), s2=(132)(465)(7)(8), s-1=(132)(465)(78), respektive t-1=(1753)(26)(4)(8).
- 3.6.5
- Elementen är id=(1)(2)(3)(4), a1=(12)(34), a2=(13)(24) och a3=(14)(23) och multiplikationstabellen blir
* id a1 a2 a3 id id a1 a2 a3 a1 a1 id a3 a2 a2 a2 a3 id a1 a3 a3 a2 a1 id - 3.7.9
- ab=(17529)(3846), ba=(14738)(2596), a2=(13)(27)(4)(5)(6)(8)(9), b2=(153)(264)(798), a-1=(1732)(49)(58)(6), respektive b-1(153)(264)(798).
- 3.7.17
- Först räknar vi ord av längd ett och två med den givna egenskapen. De tillåtna orden är , 1, respektive 01, 10 och 01. Alltså är u1=2 och u2=3.
För att gå vidare ser vi att ett ord av längd n antingen börjar med en nolla eller med en etta. Om det börjar med en nolla måste näste tecken vara en etta. Alltså måste orden antingen börja med 1 eller 01. Därefter föjler ett ord av längd n-1 respektive n-2 och det finns inget vidare krav än att detta ord inte skall innehålla konsekutiva nollor. Det finns därmed un-1 ord som börjar på 1 och un-2 ord som börjar med 01. Detta ger rekursionsformeln un=un-1+un-2, för n>2.
- 3.7.18
- Efter åtta blandningar är kortleken i ursprunglig ordning.
- 4.1.5
- 1820, 6188. (Finns svar i Biggs.)
- 4.2.2
- Det är ett oordnat urval med återläggning av tre element från en mängd med sex element. För n tärningar blir det
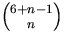 , dvs
, dvs 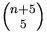 .
. - 4.3.2
- (i) 462. (ii) 45. (iii) 10. (iv) 34 560.
- 4.3.3
- Jämför koefficenten för xr i höger och vänster led. I högerledet har vi enligt binomialsatsen
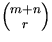 och i vänsterledet får vi när vi multiplicerar ihop de två faktorerna ett antal olika termer som innehåller xr. Vi får sådana termer när vi multiplicerar xi från den ena parantesen med xr-i från den andra. Vi får att koefficienten för xr blir summan av produkterna av koefficienterna för xi och xr-i när i går från till r.
och i vänsterledet får vi när vi multiplicerar ihop de två faktorerna ett antal olika termer som innehåller xr. Vi får sådana termer när vi multiplicerar xi från den ena parantesen med xr-i från den andra. Vi får att koefficienten för xr blir summan av produkterna av koefficienterna för xi och xr-i när i går från till r.
- 4.4.1
- 8, 6. (Finns svar i Biggs.)
- 4.4.2
- 582. (Finns svar i Biggs.)
- 4.8.2
- (i) 924. (ii) 120. (iii) 28.